Vector Calculus

On By shinynowIn Calculus

#not a rigorous illustration#

  • gradient: change of scalar quantity
  • divergence: characterizes the radiant flux of certain vector field per unit volume
  • curl: the vorticity of vector field, strength of circulation per unit area

As we are using differential calculus, changing of rate are we finding actually.

\frac{dy}{dx} means the change in y for a slight change in x. Differential means the rate of change, yet the slope. While living in three dimension world, we might encounter changing with different dimension at the same time.

That is, we introduce vector system into Calculus to manipulate change with multiple variables. And the operator for differential becomes \nabla, where

\nabla F(x,y,z) = \frac{\partial{F}}{\partial{x}}\hat{x}+\frac{\partial{F}}{\partial{y}}\hat{y}+\frac{\partial{F}}{\partial{z}}\hat{z}

Which represents the changing rate along different direction, and \nabla F(x,y,z) called the gradient of F(x,y,z), notice that the direction of gradient always point to maximum change.

The gradient of the function f(x,y) = −(cos2x + cos2y)2 depicted as a projected vector field on the bottom plane.(picture belong Wiki)

And the inner product of gradient and path becomes the difference along the path:

\nabla F(x,y,z) \cdot d\vec{S}=dF_s

Whereas sometimes we don’t care about the difference between certain position, but concern over the influence of certain continuous body on certain boundary, such as the water flowing out of tube, heat flow and electric field. Such kind of flowing can be presented by vector field, and influence of such flow often associated with inner product of surface area and current density (value depicted by vector field).

The inner product of vector field and surface area can be transferred to divergence of vector field with volume that surface enclosed. For properties which are conserved through the boundary surface, the divergence often be linked with source strength.  That is, a radiant source produces their influence, and divergence tell us how many sources or how strong the source is.

Three dimension vector field to illustrate a fluid flow with positive divergence (picture belongs to https://mathinsight.org/)

The divergence of vector field F(x,y,z) is depicted as follow:

Divergence Theorem

While sometimes the side effect of certain physic phenomenon causes rotation, such as vortex and magnetic field. We will introduce curl to illustrate how strong the whirling is. The direction of spinning is determined by right-hand-rule. Likewise, curl can be linked with source strength, except that the direction of influence is circular.

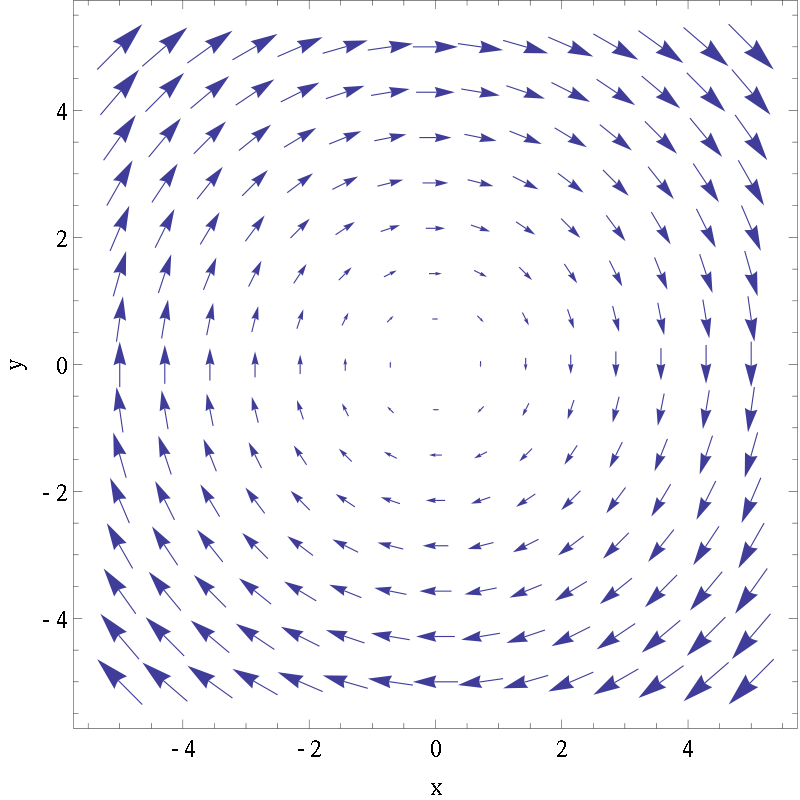
A plot of the vector field (picture by Loodog at English Wikipedia, CC BY 2.5, https://commons.wikimedia.org/w/index.php?curid=2438212)

Stoke theorem tells us that the line integral of certain vector field over certain closed loop path can be translated to a surface integral of its curl over boundary surface.

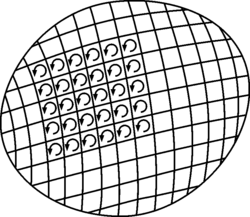
That is, we use calculus to tear a loop path into small grid (as bellow figure), and curl of vector field at that small grid represents how strong the rotation is. For a vector field with only curl without divergence, we won’t experience any influence if we traveling in ray-like path from rotation center, as nearby small vortex will cancel out that part. What curl did is like using many small cyclones to depict typhoon.

picture comes from http://mymathforum.com/calculus/45596-don-t-understand-stoke-s-theorem-revised.html

＃ 0815 Updates ＃

The curl of gradient of a scalar function is zero:
suppose you walk along the gradient, and try to walk back to start point, the line integral of gradient should always be zero, since that you have to back to origin. Thus, the curl of gradient should always be zero.

The divergence of curl is zero:
the curl of certain vector function is the perpendicular rotation part of  corresponding direction, so the divergence of curl should be zero as no parallel ingredient is included in curl.

Leave a comment